折射光向量的推导过程

Preface: 推导的起因是在阅读并实现[Ray tracing in one weekend]中的代码时遇到了一段不明所以的代码。

代码如下：

bool refract(const vec3& v,const vec3& n,float ni_over_nt,vec3& refracted)
{
    vec3 uv=unit_vector(v);
    float dt=dot(uv,n);
    float discriminant=1.0f-ni_over_nt*ni_over_nt*(1.0f-dt*dt);
    if(discriminant > 0)
    {
        refracted=ni_over_nt*(v-n*dt)-n*sqrt(discriminant);
        return true;
    }
    else
    {
        return false;
    }
}

通过查阅资料得知，这段代码是在计算折射光向量，但由于作者略去了推导过程，便很难理解其中用意。

本文以下的推导过程，是受到一篇博文的启发而完成的，在此致谢。 折射向量计算

推导过程:

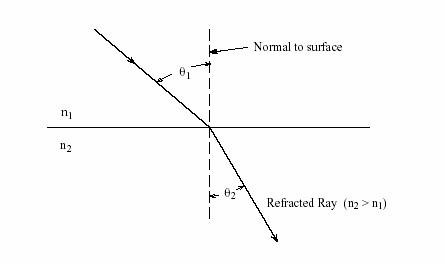
n1与n2分别是入射光与折射光所在介质的折射率。

设入射光为I，折射光为T，法线为N，垂直于平面向上，切向量G垂直于法线N，处于两种介质交界处，且方向向右。

以上所有向量均为单位向量。

显然，由于法线N与切线T互相垂直，且都是单位向量，他们组成了一组正交基，可以构成一组坐标系。所以可以将向量T分解为a*N+b*G

T = a*N + b*G

a*N是向量T在N方向的投影，所以有

又因为

联立可得

b*G是向量T在G方向上的投影，所以有

又因为

联立可得

但问题来了，切向量G尚未求出，我们应该如何得到切向量G呢？

入射光向量I在切线方向G上的投影长度为

入射光向量I在切线方向G上的分量可用向量四则运算表示为

归一化变为单位向量

所以切线向量G就推导出来了:

综上，由T = a*N + b*G可推导出:

由于折射发生时会遵循Snell’s law，入射角与折射角有如下关系：

所以前项式可化为：

由于

调换位置：

此式与书中代码所表达的意思相同，Q.E.D